Parallelschaltung von Widerständen
| Website: | Moodle, virtuelles Arbeiten und eLearning - Herzlich willkommen! |
| Kurs: | Reihen- und Parallelschaltungen (9/10) |
| Buch: | Parallelschaltung von Widerständen |
| Gedruckt von: | Guest user |
| Datum: | Mittwoch, 4. Dezember 2024, 20:05 |
1. Einleitung
Häufig verzweigen sich Leitungen und werden irgendwo wieder zusammengeführt. Den Verzweigungspunkt und den Punkt der Wiedervereinigung nennt man Knotenpunkte.
Quelle: Rolf Piffer, eigenes Werk, CC BY-SA 4.0
An den Knotenpunkten fließt etwas hinein und wieder heraus.
Da in desem Fall verschiedene Leiterstücke mit ihren Eigenschaften wie Länge, Durchmesser und spezifischen Widerstand parallel verlegt werden, ändert sich auch das Strömungsverhalten des fließenden Stoffes. Denn der Strom wird sich am Knotenpunkt zunächst aufteilen, um dann später wieder zusammenzukommen.
Welchen Effekt diese Anordnung auf den Gesamtwiderstand des parallelen Bereichs hat, ist Gegenstand dieses Buchs.
2. Die unverzweigte Leitung
Entlang einer unverzweigten Leitung muss die Stromstärke I immer gleich bleiben:
Quelle: Rolf Piffer, eigenes Werk, CC BY-SA 4.0
Denn wenn die Stromstärke links größer wäre als in der Mitte, dann müsste sich der strömende Stoff irgendwo dazwischen stauen und den Druck anwachsen lassen. Wenn hingegen die Stromstärke links kleiner wäre als in der Mitte, dann müsste auf dem Weg zur
Mitte dieser Stoff plötzlich aus dem Nichts gebildet werden.
Die verschiedenen Bereiche dieser Leitung haben verschiedene Leitungsquerschnitte und damit auch verschiedene Leitungswiderstände. Alle Teilwiderstände addieren sich zum Gesamtwiderstand. Die Leitung möge aus dem gleichen Material bestehen und somit den gleichen spezifischen Widerstand ρ haben. Der Gesamtwiderstand dieser drei Teilstücke ergibt sich als Summe der Einzelwiderstände:
Rges = R1 + R2 + R3 (1)
Rges = ρ·L1/A1 + ρ·L2/A2 + ρ·L3/A3 = ρ · ( L1/A1 + L2/A2 + L3/A3)
Das Leitungsstück mit dem höchsten Quotienten L/A trägt am meisten zum Gesamtwiderstand bei. D.h. das Stück mit dem kleinsten Durchmesser und der größten Länge.
Da die Stromstärke in einer Schaltung als
I = U / R (siehe Kapitel "Stromstärke und Widerstand")
geschrieben werden kann, folgt mit der Gleichung (1) für den dargestellten Fall:
I = U / (R1 + R2 + R3 ) (2)
Die Stromstärke nimmt mit jedem neuen Widerstand in der Leitung weiter ab.
Gleichung (2) wird nach der Spannung U aufgelöst:
U = (R1 + R2 + R3 ) · I = R1 · I + R2 · I + R3 · I
Das ist wieder die bekannte Maschenregel:
U =U1 + U2 + U3
In allen in diesem Buch behandelten Fällen wird davon ausgegangen, dass die elektrischen Verbindungsleitungen selbst einen nur vernachlässigbaren Widerstand haben.
3. Die verzweigte Leitung
Gibt es aber Punkte, an denen sich der Strom auteilen kann, spricht man von einer Parallelschaltung von Widerständen.
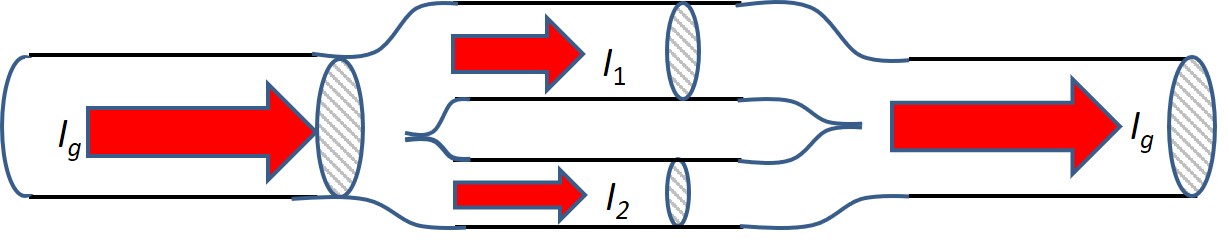
Quelle: Rolf Piffer, eigenes Werk, CC BY-SA 4.0
Der Strom teilt sich so auf, dass der größere Teil der Stromstärke durch den Zweig strömen wird, der auch den kleineren Widerstand dem Strom entgegensetzt.
Mit jedem weiteren Zweig kann insgesamt noch mehr Stoff durch die Leitung strömen:
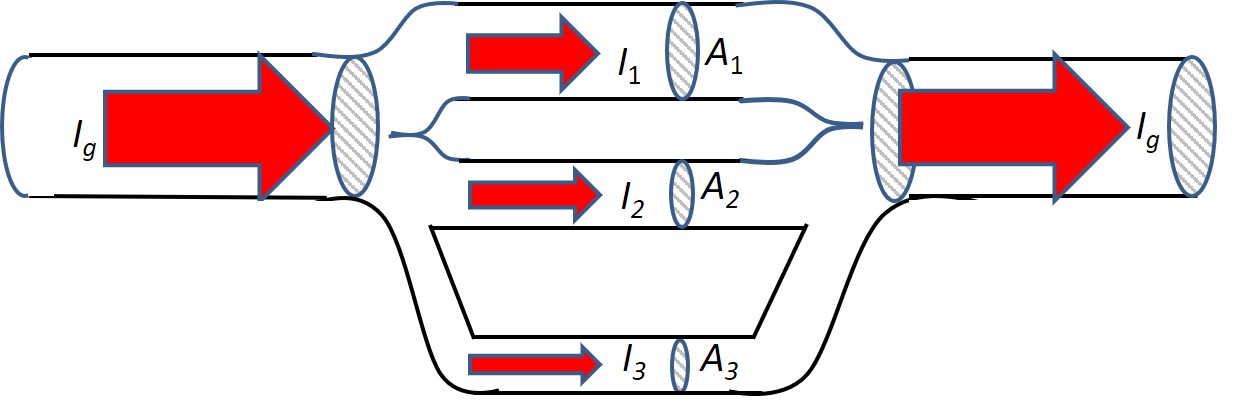Quelle: Rolf Piffer, eigenes Werk, CC BY-SA 4.0
Der Bereich, in dem die Leiter parallel angeordnet sind, hat mit wachsender Zahl an Zweigen einen immer kleineren Widerstand, weil sich der Strom auf immer mehr Leitungen verteilen kann.
Betrachtet man nur den mittleren Teil mit den parallel geschalteten Leitungen:
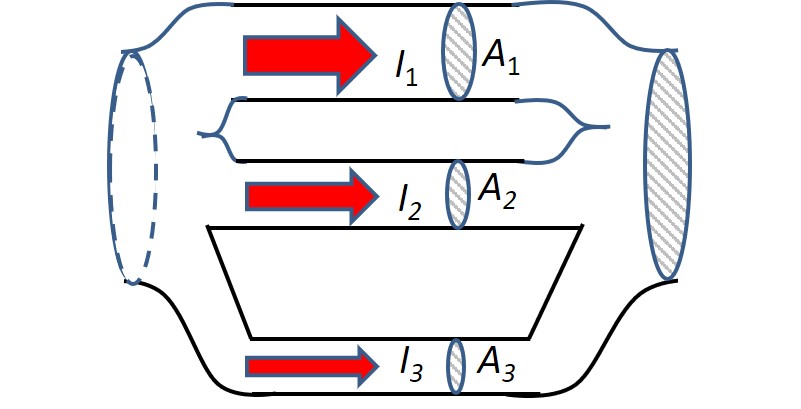
Quelle: Rolf Piffer, eigenes Werk, CC BY-SA 4.0
Alle Leitungen sind gleich lang und links und rechts miteinander verbunden. Somit ist die Druckdifferenz zwischen den Enden der parallel geschalteten Leitungen auch gleich:
Δp1 = Δp2 = Δp3 = ΔpDa die gesamte Querschnittsfläche A dieses Teils immer größer wird, je mehr Leitungen parallel verlegt sind, wird die gesamte Querschnittsfläche Ages immer größer. Damit wird der Gesamtwiderstand wegen
R = ρ∙L/Ages mit jeder parallelen Leitung immer kleiner.
Für den Fall einer Parallelschaltung von elektrischen Widerständen R1 bis R3 ergeben sich analoge Überlegungen.
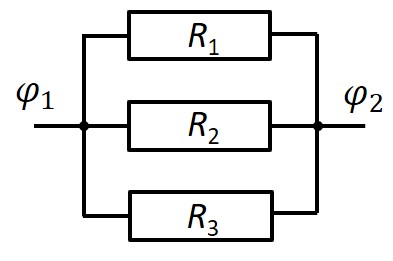
Quelle: Rolf Piffer, eigenes Werk, CC BY-SA 4.0
Die Spannung ist an allen parallel geschalteten Widerständen gleich:
U = φ2 - φ1 = U1 = U2 = U3
Durch jeden Widerstand dieser Parallelschaltung fließt ein Strom, der abhängig vom jeweiligen Widerstandswert ist. Alle diese parallelen Ströme entstehen aus dem in den Knoten hinein fließenden Gesamtstrom. Die Gesamtstromstärke Iges ergibt sich als Summe aus allen Teilströmen in den parallelen Zweigen:
Iges = I1 + I2 + I3
4. Gesamtwiderstand
Bei drei parallelgeschalteten Widerständen ergibt sich sich die Gesamtstromstärke zu
Iges = I1 + I2 + I3 (1)
Und mit I1 = U / R1 , I2 = U / R2 , I3 = U / R3 und Iges = U / Rges
kann man den Gesamtwiderstand Rges nach Gleichung (1) berechnen:
U / Rges = U / R1 + U / R2 + U / R3 = U· (1/R1 + 1/R2 + 1/R3 ) oder
1/Rges = 1/R1 + 1/R2 + 1/R3
Für den besonderen Fall, dass alle drei Widerstände den gleichen Wert haben
(R1 = R2 = R3 = R), ergibt sich der einfache Fall:
1/Rges = 3/R oder
Rges = R/3
Der Wert des Gesamtwiderstands ist hier nur noch ein Drittel so groß wie der Widerstandswert eines einzelnen Widerstands.
Der Gesamtwiderstand bei einer Parallelschaltung von Widerständen wird kleiner als jeder einzelne dieser Widerstände.
4.1. Übung 1
Beide Lampen haben den gleichen elektrischen Widerstand von 20 Ω. Die Batterie liefert eine Spannung von 6 V.
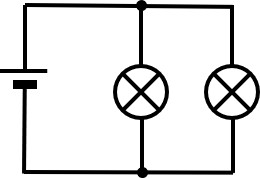Bestimme die Gesamtstromstärke von und zur Batterie.
4.2. Lösung zur Übung 1
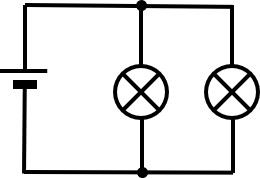An beiden Lampen liegt die Batteriespannung von 6 V an. Beide Lampen haben den gleichen Widerstand.
Jeder Zweig hat einen Widerstand von 20 Ω. Damit fließt durch jeden Zweig der gleiche Strom von
I = U / R = 6 V / 20 Ω = 0,3 A
Damit ergibt sich eine Gesamtstromstärke von Iges = I1 + I2 = 0,6 A
4.3. Übung 2
Alle Lampen der abgebildeten Schaltung haben den gleichen Widerstand von 20 Ω. Die Batterie liefert eine Spannung von 6 V.
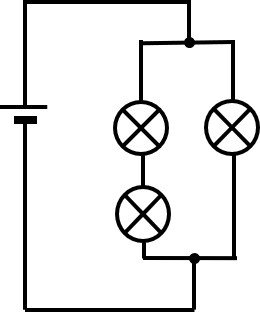Bestimme die Gesamtstromstärke von bzw. zur Batterie.
4.4. Lösung zur Übung 2
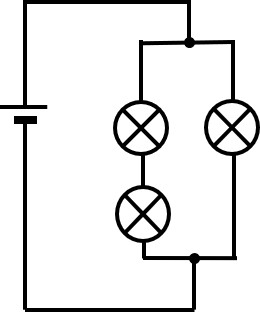Da alle Lampen den gleichen Widerstand von 20 Ω haben, und die Widerstände im linken Zweig in Reihe geschaltet sind, addieren sich diese beiden zum Gesamtwiderstand im linken Zweig:
Rlinks = 40 Ω
Daher fließt durch den linken Zweig ein Strom von
Ilinks = 6 V / 40 Ω = 0,15 A
Durch den rechten Zweig ist die Stromstärke doppelt so groß, weil bei gleicher Spannung der Widerstand mit 20 Ω nur halb so groß ist: Irechts = 0,3 A.
Damit beträgt die Gesamtstromstärke 0,45 A.
5. Aufgaben zu gemischten Schaltungen
In dem folgenden Abschnitt wird auch experimentell gezeigt, wie ähnlich sich Wasserstromkreise und elektrische Stromkreise verhalten.
Die Überlegungen zu auch komplexeren Schaltungen lassen sich anhand von einem dazu passenden Wasserstromkreismodell sehr anschaulich machen.
Nehmen wir zum Beispiel die folgenden zwei Schaltungen:
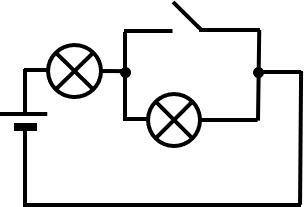
Abb. 1: Schaltung 1, beide Lampen haben den gleichen Widerstand
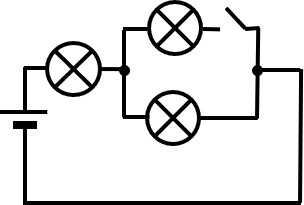
Abb. 2: Schaltung 2, alle Lampen haben den gleichen Widerstand
Quelle: Rolf Piffer, eigenes Werk, CC BY-SA 4.0